Clase Hashtable

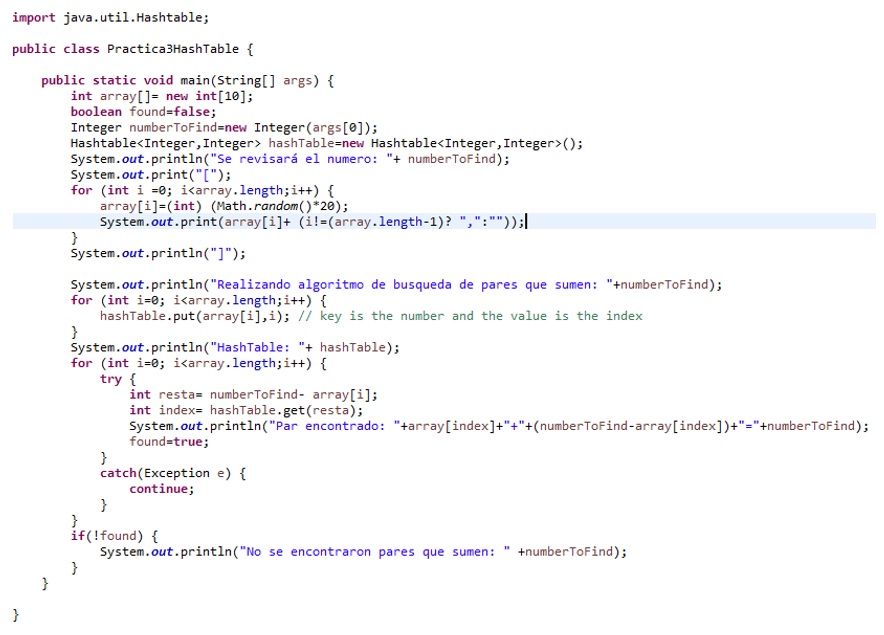
El código es igual al anterior hasta la línea en la que se insertan valores en la Hashtable. Una Hashtable tiene la peculiaridad de almacenar valores por pares clave-valor; de tal manera que se accede al valor mediante la clave. Dicha clave es única, es decir, no pueden existir claves repetidas en una Hashtable, en caso de intentar insertar dos claves iguales, lo que hará la estructura es actualizar el valor de la clave. Para esta solución se almacenará el valor del arreglo como la clave y el índice de donde está ubicado como el valor, ejemplo:

De tal manera que para acceder al valor “0” se usará la llave “2” y la hashtable regresará el 0; si se usa la llave 5 se regresará el valor 1, etcétera, es decir, se obtiene el índice mediante el valor.

Una vez que se ha llenado la Hashtable, se procede a realizar un ciclo sobre el arreglo original y se usa la línea “hashTable.get(numberToFind-array[i])!=i” para determinar si dentro de la Hashtable existe un número que sea la resta del número a buscar menos el número actual del arreglo. De existir, se puede asegurar que hay un par que números que cumplen con la restricción de la suma (de no existir se controla un error con un bloque try-catch que se verá en próximas prácticas).

Las pruebas de escritorio que se muestran a continuación permiten visualizar de forma más clara el funcionamiento del algoritmo.

Ejecución y pruebas de escritorio

Primero se hará una prueba de escritorio para entender una Hashtable, es decir, el ciclo for que tiene la línea hashtable.put(array[i],i);

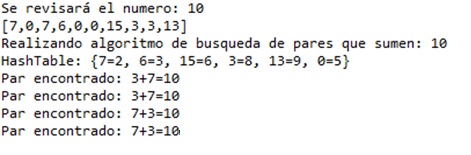
Se generó el arreglo:

el cual se insertará en la Hashtable:

Debido a que la Hashtable no repite llaves, se insertan seis elementos. En la tercera iteración se puede apreciar que la llave 7 ya existía y lo que se hace es actualizar el valor de 0 a 2, hay que recordar que este valor indica “el índice donde el número 7 es encontrado”; por lo tanto, sólo necesitamos almacenar dicha información una vez, ya que lo importante es saber que existe un 7 y se obtiene un índice para poder acceder a él utilizando el arreglo principal.

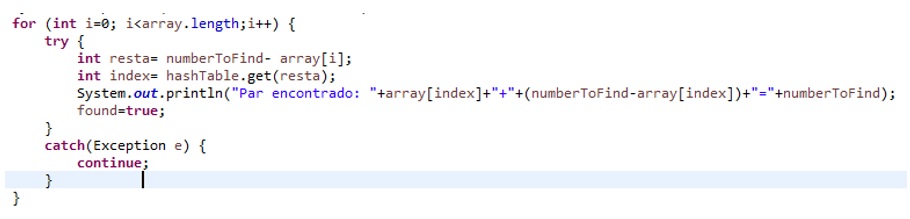
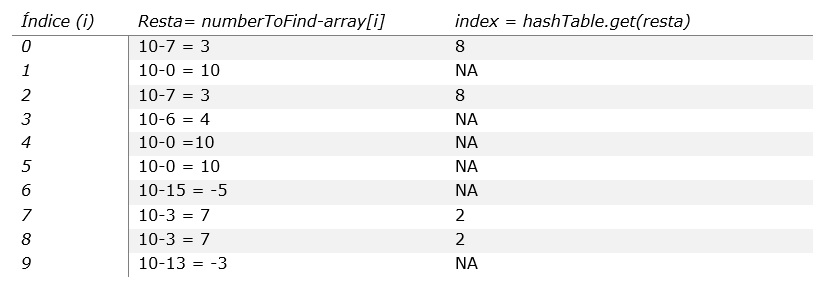
Procedemos a la segunda parte del algoritmo que es la parte donde se determina si existe o no un par (de momento ignorar el bloque try-catch, se explicará en futuras prácticas):

Como se puede observar en la tabla, los casos donde aparece NA son imposibles debido a que el índice obtenido de la Hashtable es inexistente; por ejemplo, en la iteración 1 se intenta acceder la llave 10 en el Hashtable. Dicha llave no existe (revisar la primera tabla de pruebas de escritorio) y, por lo tanto, se descarta que exista un 0 que cumpla con la condición “10-0 = 10”, en caso de que el índice sí exista, se habrá encontrado un par.

Más ejemplos de ejecución del programa:

Si bien este método de solución parece complicar más un problema sencillo, se deja a discreción del alumno el comparar los tres métodos de solución (fuerza bruta, List y Hashtable) cambiando la longitud del arreglo principal (int array[ ]= new int[10];) a valores más grandes como 1000 o superiores y observar las ventajas de cada método. Aunado a lo anterior, se recomienda revisar otras colecciones para intentar dar solución al mismo problema. En actividades posteriores será requisito usarlas (se indicará en su momento) para distintas tareas.