Introducción
La lógica es la ciencia que estudia las formas, estructuras y esquemas del pensamiento humano (Arnaz, 1988), es decir, estudia las formas del razonamiento. Algunas de las principales razones para estudiar lógica son las siguientes:
• Desarrollar habilidades de análisis y abstracción.
• Adquirir destreza en el razonamiento matemático.
• Minimizar las ambigüedades en el lenguaje.
Por lo tanto, la lógica es esencial para la resolución de problemas, en disciplinas tan críticas como las matemáticas y la computación.
Más allá de ser una herramienta teórica, su estudio permite desarrollar habilidades fundamentales, como el análisis, la abstracción y el razonamiento matemático, todas indispensables en la era digital actual, en donde la precisión y claridad son clave para manejar grandes volúmenes de información.
Hoy en día, las aplicaciones de la lógica son más relevantes que nunca. Desde el diseño de algoritmos eficientes que optimizan procesos, hasta la seguridad en sistemas informáticos que protegen datos sensibles, la lógica es un pilar que sustenta el avance tecnológico.
Comprenderla no sólo te dará una ventaja competitiva, sino que te permitirá resolver problemas complejos de manera eficaz y con mayor rigor.
En este tema nos concentraremos en revisar, principalmente, la utilidad de la lógica para las matemáticas y la computación, ramas del conocimiento en las que son indispensables las habilidades de análisis y abstracción. Por un lado, las matemáticas son la abstracción de la realidad que permite la resolución de problemas, y por el otro, en la computación, los desarrolladores necesitan analizar las propiedades lógicas de los sistemas que desarrollan, especialmente porque estos sistemas suelen manejar información económica, de seguridad, de procesos y de manejo de datos (Farré et al., 2013).
Por lo tanto, se abordarán los conceptos fundamentales de la lógica y su importancia como herramienta para resolver problemas mediante las matemáticas y la programación en distintas situaciones.
Prepárate para descubrir cómo el pensamiento lógico te abre las puertas a nuevas formas de entender y transformar el mundo.
Objetivo
Reconocer los principios de la lógica matemática como herramienta para el desarrollo de habilidades de análisis y abstracción, mediante la presentación de los elementos fundamentales y áreas de aplicación en las matemáticas y la computación.
¿Qué es la lógica?
La lógica es una disciplina que, por medio de reglas y técnicas, determina si un argumento es válido. En matemáticas sirve para demostrar teoremas, inferir resultados y resolver problemas. En computación se usa para automatizar procesos, desarrollar y revisar programas, manejar bases de datos y estudiar lenguajes formales (Jiménez, 2014), entre otros aspectos. En general, la lógica se emplea para estructurar el conocimiento y evitar ambigüedades en el lenguaje.
El aprendizaje de la lógica nos permite desarrollar una forma objetiva de razonar; con esta herramienta es posible modelar problemas hipotéticos y resolverlos sin la subjetividad del juicio humano, lo que representa la base de la inteligencia artificial (IA).
Evolución de la lógica
En el desarrollo histórico de la lógica pueden diferenciarse tres etapas:
- Aplicación a la filosofía (hasta 1700 con Leibniz), para validar argumentos.
- Aplicación a las matemáticas (desde el siglo XIX), para sustentar las teorías matemáticas y definir los teoremas.
- Aplicación a la computación (desde 1960), para automatizar la solución de problemas y el razonamiento humano.
La lógica se inició como una herramienta para esquematizar las formas de razonamiento; ejemplo de ello fue Tomás de Aquino, quien la empleó como vehículo de transparencia en las discusiones teológicas. Más adelante Leibniz formuló la lógica como cálculo de razones para servir de base a las teorías matemáticas.
La idea de Leibniz se comenzó a aplicar a mediados del siglo XIX, con los trabajos de De Morgan y con la publicación de The law of thought, de G. Boole, que proponía un cálculo algebraico de significado bivalente. Esto recibió un fuerte impulso con la aportación de G. Fregge y su formulación del cálculo de predicados. A estos trabajos siguen los de Whitehead y Russel, Hilbert, Herbrand, Tarski y Gödel, con su teorema de incompletitud, que constituyeron la base teórica, tanto sintáctica como semántica, de la lógica matemática (Cuena, 1986). A partir de esto, la lógica matemática brindó las bases para las ciencias de la computación: programación, circuitos electrónicos, sistemas expertos e inteligencia artificial, principalmente.
-400
Primera etapa
La lógica, como ciencia que estudia el razonamiento, nació con los filósofos griegos.
-348
Inicio formal de la lógica con Aristóteles
Aplicación de la lógica a la filosofía.
1252-1274
Santo Tomás de Aquino
Desarrolló una serie de obras en las que empleaba la lógica para resolver el juicio.
1620
Francis Bacon
Aporta el método experimental inductivo.
1637
René Descartes
En su obra Discurso del método para dirigir bien la razón y hallar la verdad de las ciencias, formuló las reglas lógicas para el descubrimiento de la verdad.
1680 - 1700
Segunda etapa: Leibniz
Aplicación a la matemática para demostrar la validez a partir de reglas. Introdujo las bases de la lógica proposicional con su “lenguaje binario”.
1847
Augustus de Morgan
Lógica formal.
1847
George Boole
En su obra The laws of thought propuso un cálculo algebraico de significados.
1879
Frege
Nace la “nueva lógica”. Padre de la lógica matemática y la filosofía analítica.
1900
Tercera etapa: Siglo XX
Aplicación de la lógica a la computación.
1914
Whitehead y Russel. Principia Mathematica
Demostrar la matemática a partir de axiomas.
1930
Herbrand y Tarski
Fundamentan el enfoque semántico.
1936
Kurt Gödel
Teorema de incompletitud del enfoque axiomático.
1956
Conferencia de Darmouth College
Se plantean los objetivos de una clase de aplicaciones de programación que incorporan modelos.
1965
Robinson
Regla universal de resolución con unificación.
1970
Revitalización de la lógica
Con la aparición de las computadoras se hacen formulaciones en inteligencia artificial.
1972
Colmerauer produjo el sistema Q
Antecedente del lenguaje Prolog en 1975.
Habilidades que desarrolla el aprendizaje de la lógica
Razonamiento deductivo
El razonamiento deductivo consiste en construir argumentos sólidos para obtener conclusiones lógicas, a partir de premisas.
Esta competencia es fundamental, no sólo en el desarrollo de teorías matemáticas y algoritmos computacionales, sino en situaciones cotidianas, como evaluar la validez de un argumento, tomar decisiones informadas y resolver disputas lógicas en debates o negociaciones.
Actividad 1. Identificación de habilidades
Las habilidades cognitivas esenciales para el pensamiento crítico y la resolución de problemas son las siguientes:
Estas habilidades son fundamentales, no sólo en el ámbito académico, sino también en la vida cotidiana y profesional; además, te permitirán analizar situaciones complejas, tomar decisiones informadas y defender tus puntos de vista de manera lógica y estructurada.
Capacidad de abstracción
Es mediante un proceso de abstracción que el conocimiento se representa en modelos, ecuaciones o programas, a partir de los cuales se resuelven de forma objetiva (válida) los problemas.
Cuatro amigos: Arturo (A), Beatriz (B), Carlos (C) y Daniel (D) son sospechosos de plagio. Ellos testifican lo siguiente:
¿Quién es el culpable?
La capacidad de abstraer implica identificar los elementos esenciales de un problema, ignorando los detalles irrelevantes, para formular una representación simplificada pero precisa:
“Todo número entero tiene neutro multiplicativo:
{∀x ∈ ℤ, ∃y =1|x ∗ y = x }”
Esta habilidad es fundamental en el diseño de software, la creación de modelos matemáticos y la resolución de problemas en diversas disciplinas, como la economía, los negocios, la física y la ingeniería.
Argumentación
La argumentación es la capacidad de construir, presentar y defender argumentos lógicos y coherentes de forma sólida. Implica no sólo la formulación lógica de un punto de vista basado en evidencias, sino también la capacidad de refutar contraargumentos, empleando herramientas de la lógica; por ejemplo, el uso de silogismos, la identificación de falacias o sofismos y la construcción de pruebas formales, herramientas empleadas en juicios orales y en el ejercicio de la abogacía.
La argumentación es crucial en la redacción de ensayos, artículos académicos y presentaciones, en donde es necesario presentar un punto de vista, respaldarlo con evidencia y llegar a conclusiones coherentes. Esta habilidad es importante para resolver problemas mediante programas computacionales o realizar búsquedas y generar reportes en bases de datos.
Resolución de problemas complejos
La lógica matemática entrena a los estudiantes para descomponer problemas complejos en partes más manejables, identificar relaciones entre variables y aplicar soluciones sistemáticas. Ejemplo de esto es la programación orientada a objetos.
Esta habilidad es indispensable en áreas como la ingeniería, la investigación científica y la gestión de proyectos, en donde los problemas suelen ser multifacéticos y requieren un enfoque estructurado; además, en el ámbito profesional, la capacidad para resolver problemas complejos es altamente valorada, ya que permite a las personas abordar desafíos de manera eficiente y creativa.
Operadores lógicos
El elemento básico de la lógica son las proposiciones, con las cuales se modela el conocimiento con ayuda de operadores (conectivos). A partir de estas proposiciones y mediante reglas de inferencia se genera nuevo conocimiento.
La negación se representa con cualquiera de las siguientes notaciones: −p, ¬p, ∼p o p ’ o NOT.
Ejemplo
El 7 es número primo (Verdadero)
El 7 NO es número primo (Falso)
Ejemplo
K = 20 && Tol < 0.0003
Ejemplo
Un triángulo es equilátero si todos sus lados son iguales o todos sus ángulos internos son iguales.
Se denota con p ∨ q y tiene el valor de verdad falso cuando p y q tienen los mismos valores de verdad. Indica “o uno o el otro, pero no ambos”. En programación XOR.
Ejemplo
México está en América o en Europa.
Se expresa como p → q, en donde “p ” y “q ” son proposiciones lógicas; a p se le denomina antecedente o hipótesis y a q se le denomina consecuente o tesis. Se lee “si p entonces q ”. En programación se denominan instrucciones condicionales; la más común es IF. Se define de manera que la proposición p → q es falsa sólo cuando p es verdadera y q es falsa. En cualquier otro caso es verdadera.
Ejemplo
If sum == 20 print (“Serie completada”)
Si x
Dadas dos proposiciones p y q, la bicondicional o doble implicación, denotada por p ↔ q, se lee “p si y sólo si q ”, “p es equivalente a q ” o “p es condición necesaria y suficiente para q ”; se define de modo que es verdadera si y sólo si p y q tienen el mismo valor de verdad.
Ejemplo
Supongamos las siguientes dos proposiciones:
• p : "El número es par".
• q : "El número es divisible por 2".
La bicondicional p ↔ q se puede leer como…
"El número es par si y sólo si es divisible por 2".
"El número es par y es equivalente a que el número sea divisible por 2".
Actividad 2. Familiarización con los conectivos
Los conectivos lógicos son herramientas fundamentales en la lógica y las matemáticas, ya que nos permiten construir proposiciones complejas a partir de proposiciones simples.
Aplicaciones prácticas en computación
Diseño de algoritmos
Dado que el algoritmo es una secuencia finita de instrucciones bien definidas para realizar una tarea, las leyes y operadores de la lógica permiten formular condiciones que controlan el flujo del algoritmo y la generación de resultados correctos. Algunos ejemplos de algoritmos que hacen uso de operadores lógicos, ciclos (mientras, para), expresiones lógicas y valores de verdad son los siguientes:
Búsqueda binaria (encontrar un elemento en una lista ordenada)
Ordenar una lista de datos
Realizar búsquedas específicas en una base de datos
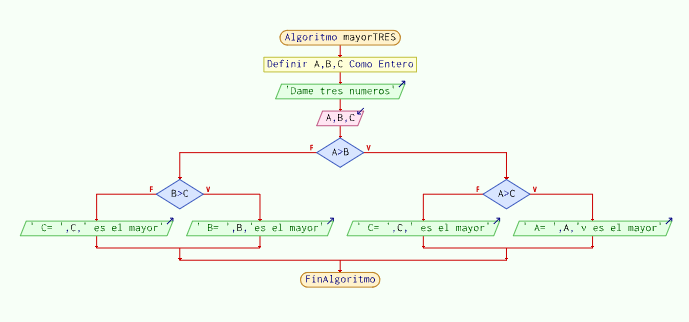
Sistemas expertos
Los sistemas expertos basados en reglas lógicas (condicionales) imitan la toma de decisiones humanas. Ejemplos de sistemas expertos que trabajan a partir de condicionales:
• Sistemas de respuesta automatizada para llamadas de servicio o de consulta.
• Sistemas de sugerencia de plan nutricional o de ejercitación, de acuerdo al perfil del usuario definido a partir de la información proporcionada
Validación de software
La validación de software asegura que un programa cumple con sus especificaciones y funciona correctamente en todos los casos posibles. La lógica nos proporciona técnicas para probar que un programa cumple con sus especificaciones. También es útil en confirmaciones lógicas para verificar qué partes específicas del código funcionan como se espera. Ejemplo:
Lógica de Hoare: Es una extensión de la lógica de predicados de primer orden para razonar sobre la corrección de programas imperativos construidos sobre una signatura (González, 2016).
Criptografía
Los algoritmos criptográficos utilizan operaciones lógicas como AND, OR y XOR para transformar datos en formas que son difíciles de interpretar sin una clave. La seguridad de un sistema criptográfico se basa en su resistencia a ataques, lo cual se puede analizar utilizando principios de lógica matemática.
Ejemplo:
Algoritmo RSA: Algoritmo de cifrado que se basa en la dificultad de factorizar números grandes en productos de primos. Utiliza la teoría de números y la lógica matemática para asegurar la confidencialidad de los datos.
Bases de datos
Las bases de datos, como concentrados de datos organizados, requieren de la lógica matemática para manipular y consultar los datos. Operaciones como unión, intersección y selección se basan en principios lógicos; además, la lógica se utiliza para garantizar la consistencia de los datos (integridad referencial) y para construir consultas complejas que extraen información específica.
Ejemplo:
Consultas SQL: En el lenguaje de consulta SQL, operaciones como SELECT, JOIN, y WHERE se basan en operaciones de lógica proposicional; por ejemplo, una consulta que combina datos de varias tablas y filtra resultados según ciertas condiciones.
Diseño de circuitos
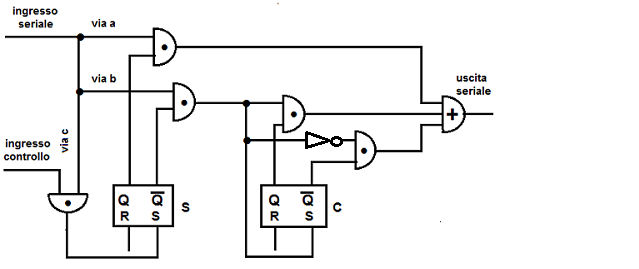
El diseño y construcción de circuitos eléctricos está basado en su totalidad en los operadores lógicos, debido a que todo se trata de encendido/apagado, es decir, lógica bivalente. Estos circuitos son la base de los dispositivos electrónicos que empleamos en el día a día.
Inteligencia artificial
Actualmente, la inteligencia artificial ha tomado fuerza mediante aplicaciones computacionales que generan respuestas a partir de bases de datos y sistemas de búsqueda que emplean la lógica.
Otro ejemplo son los sistemas de recomendación, los cuales aplican la lógica difusa para hacer recomendaciones basadas en patrones de comportamiento del usuario; por ejemplo, un sistema de recomendación de películas puede sugerir una película con base en preferencias vagas, como "me gusta la acción y la ciencia ficción".
Actividad 3. Aplicaciones de computación
Las aplicaciones de computación son herramientas que permiten al usuario realizar operaciones o funciones específicas; entre ellas, los algoritmos hacen uso de operadores lógicos para la generación de resultados correctos, mientras los sistemas expertos imitan la toma de decisiones humanas.
Conclusión
Al aprender lógica matemática, se adquieren herramientas teóricas y prácticas para resolver problemas y entender asignaturas más complejas, y se desarrollan habilidades cognitivas que transforman la forma de razonar y usar los recursos cognitivos, principalmente en la resolución de problemas. La apropiación de las habilidades y conocimientos de la lógica matemática permitirá desarrollar habilidades en la programación y dar sustentos formales para materias como Teoría de la Computación, Sistemas Expertos e Inteligencia Artificial, además para innovar y aplicar sus conocimientos en el desarrollo de tecnologías avanzadas y en la resolución de desafíos del mundo actual.
Autoevaluación. La lógica matemática
La lógica matemática es un pilar fundamental, tanto en matemáticas como en computación; ya hemos revisado todos sus beneficios; además, los operadores lógicos son herramientas esenciales para procesar información y tomar decisiones en algoritmos y sistemas computacionales.
Fuentes de información
Bibliografía
- Arnaz, J. A. (1988). Iniciación a la lógica simbólica. Trillas.
- Cuena, J. (1986). Lógica informática (2.ª ed.). Alianza.
- Farré, R., Nieewenhuis, R., Nivela, P., Oliveras, A., Rodríguez, E. y Sierra, J. (2013 Lógica para informáticos. Alfaomega.
- González, N. (2016). Verificación formal de la lógica de Hoare en Isabelle/HOL. Universidad de Sevilla.
- Jiménez, J. A. (2014). Matemáticas para la computación. Alfaomega.
Documentos electrónicos
- RoleCatcher. (2024). Biblioteca de habilidades de RoleCatcher: crecimiento para todos los niveles. https://rolecatcher.com/es/habilidades/conocimiento/artes-y-humanidades/humanidades/logica/
- UNAM. (2013). Apoyo académico para la educación media superior. http://objetos.unam.mx/
Cómo citar
Carrillo, T. y López, A. (2025). La lógica matemática como la base del pensamiento analítico para las matemáticas y la computación. Unidades de Apoyo para el Aprendizaje. CUAED/Facultad de Estudios Superiores Acatlán-UNAM. (Vínculo)