¿Sabes qué es un centroide, cómo se obtiene y por qué es tan importante conocerlo?
La estática es la parte de la física que ha interesado a la arquitectura de todos los tiempos; es parte de la mecánica y trata del equilibrio.
En este contexto, el centroide, de un objeto cualquiera, es el punto que define su centro geométrico, el cual se obtiene con el uso de ecuaciones de equilibrio.
Perspectiva en edificios
Tomada de https://es.storyblocks.com/stock-image/modern-buildings-shot-from-a-low-angle-during-the-evening-rywgvivcboiskjqohe
De las múltiples formas planas geométricas, nos ocuparemos de las figuras regulares: el rectángulo, el triángulo y la elipse [y sus variantes más usuales (en fracciones de círculo)], ya que de ellas se conocen fácilmente sus centroides, mismos que se encuentran en todas las publicaciones relativas al tema, tanto en papel, como cibernéticas.
A continuación, se representan las coordenadas de los centroides en dichas superficies.
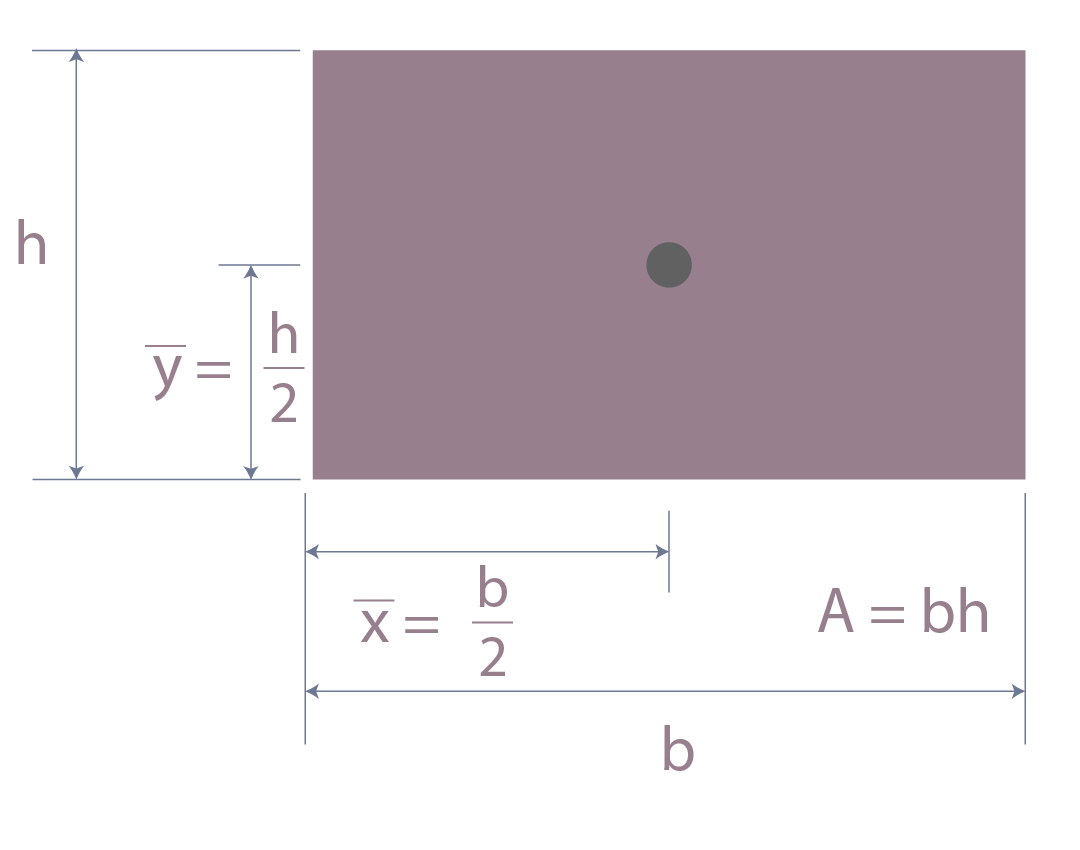
Coordenadas de centroide para réctangulo
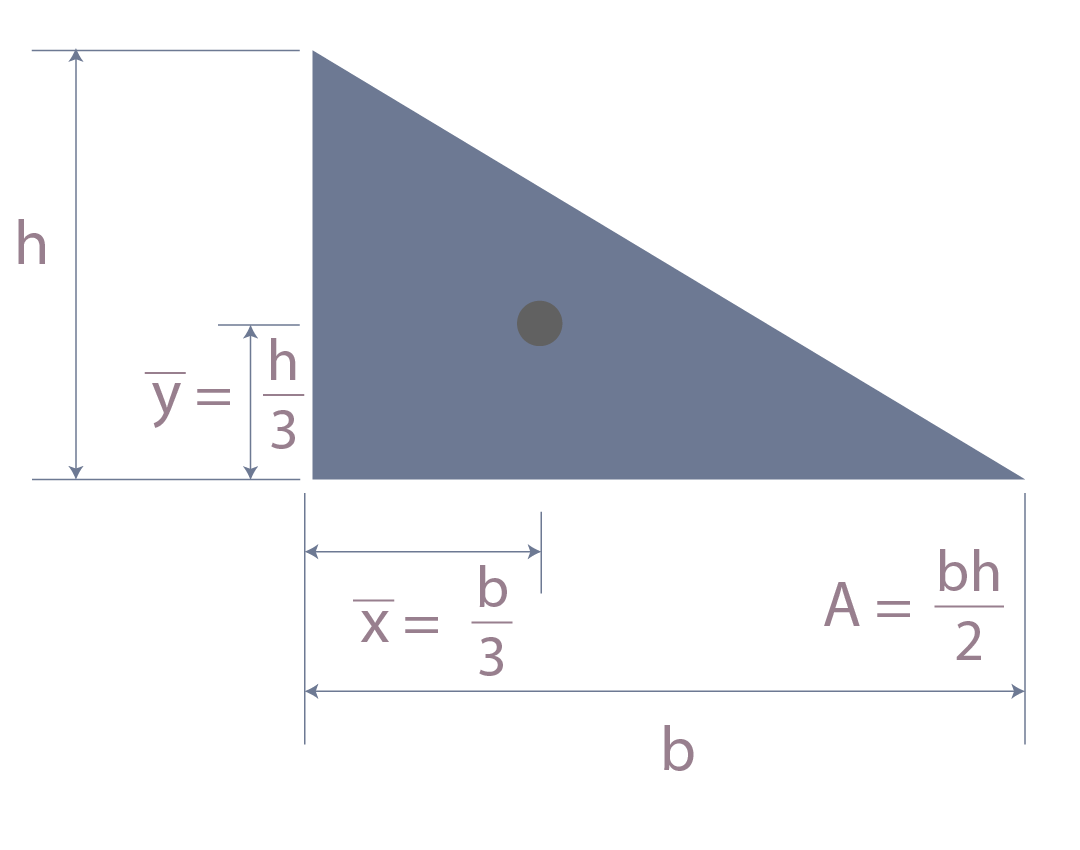
Coordenadas de centroide para triángulo rectángulo
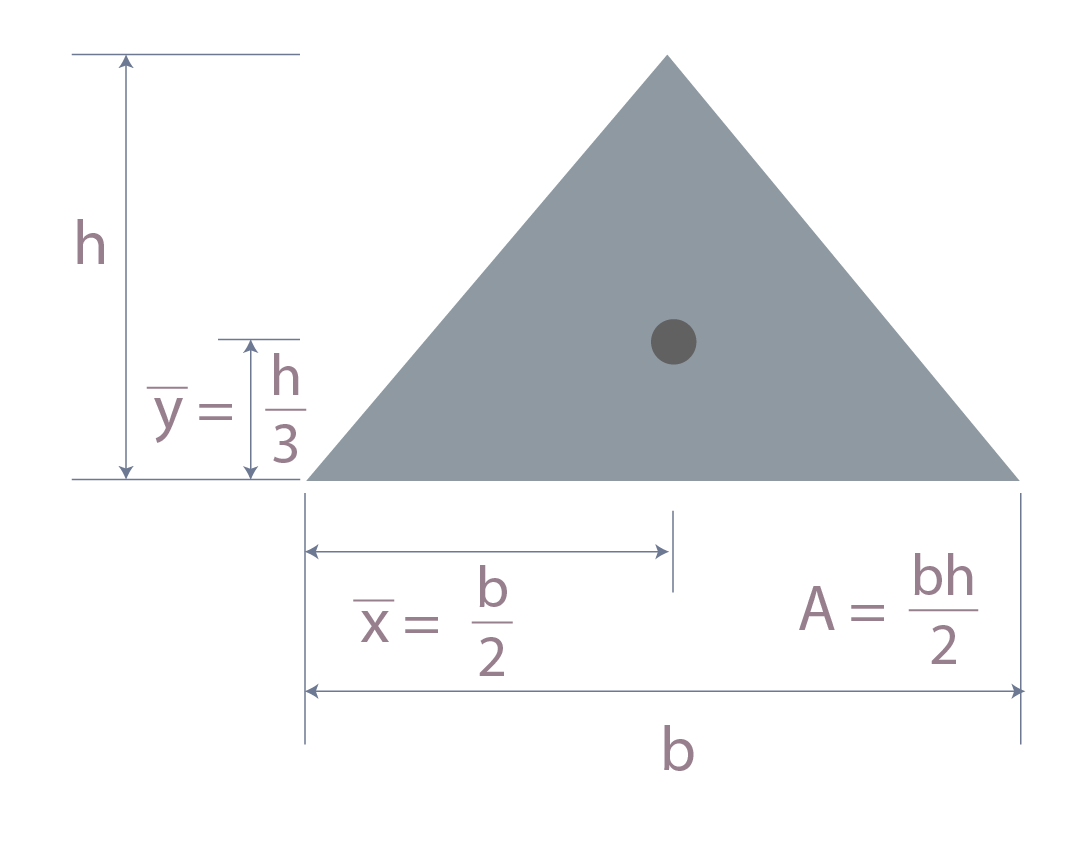
Coordenadas de centroide para triangulo isósceles.
Coordenadas de centroide para círculo.
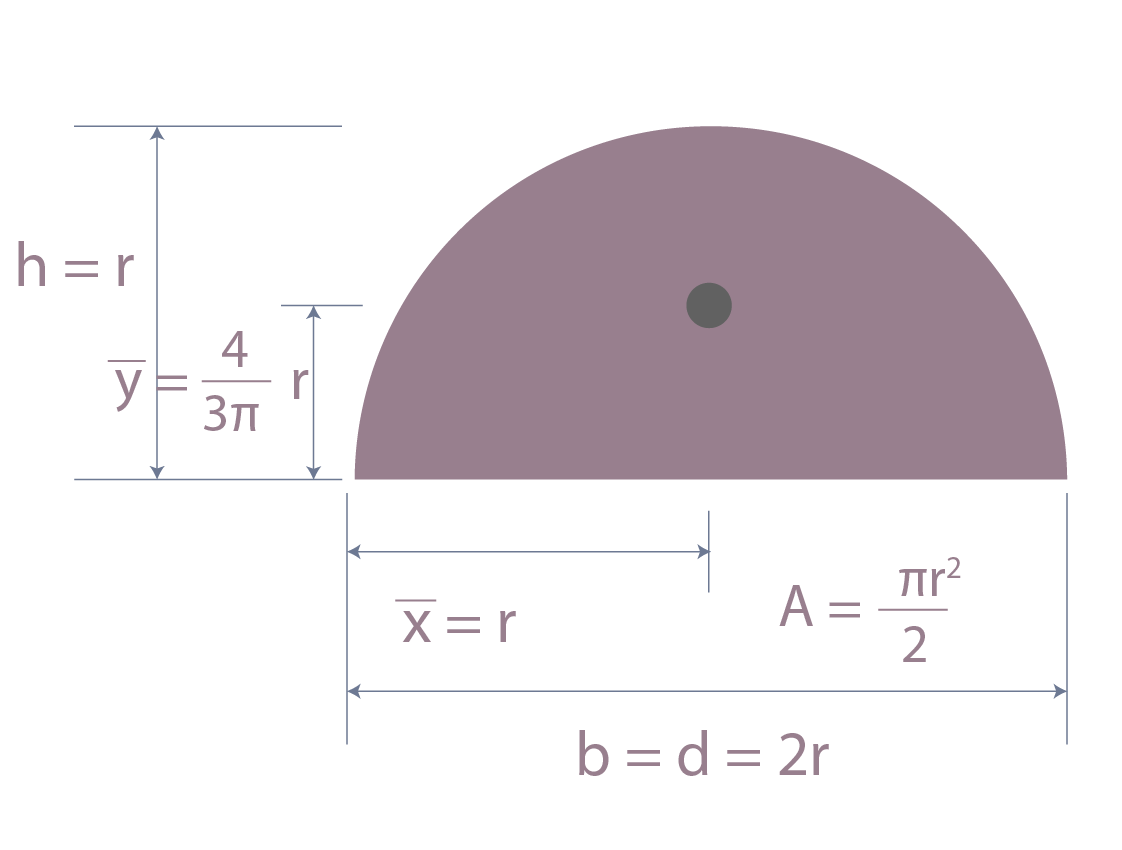
Coordenadas de centroide para semicírulo.
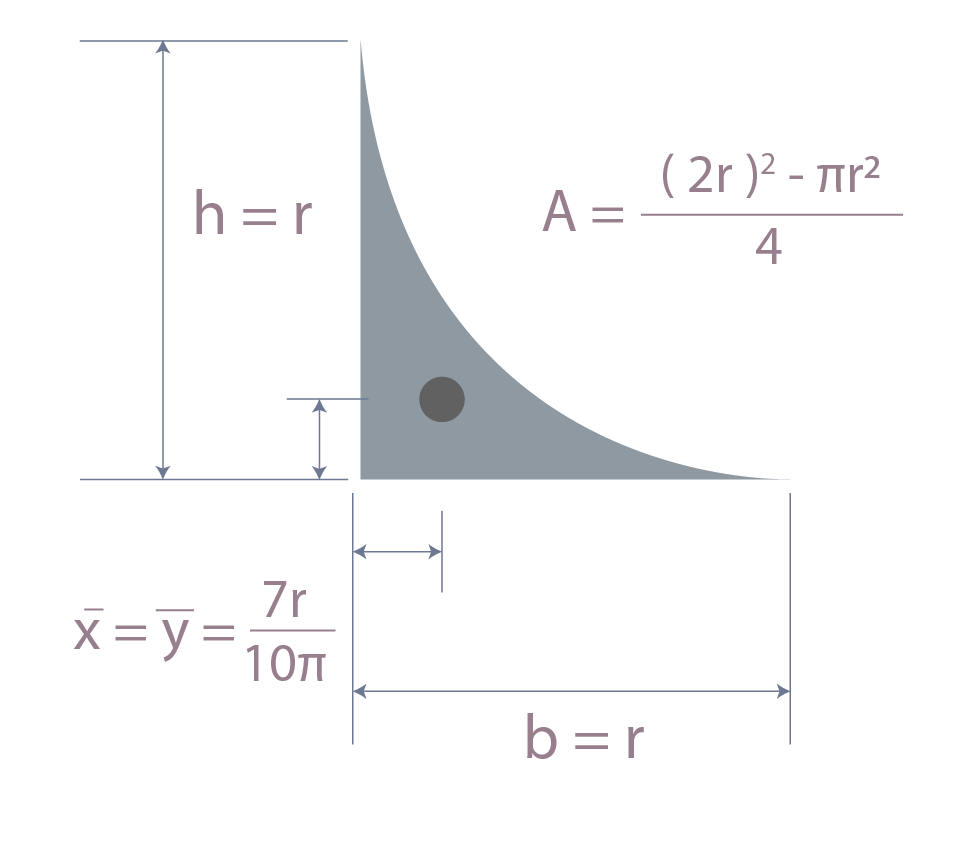
Coordenadas de centroide para ¼ de círculo.
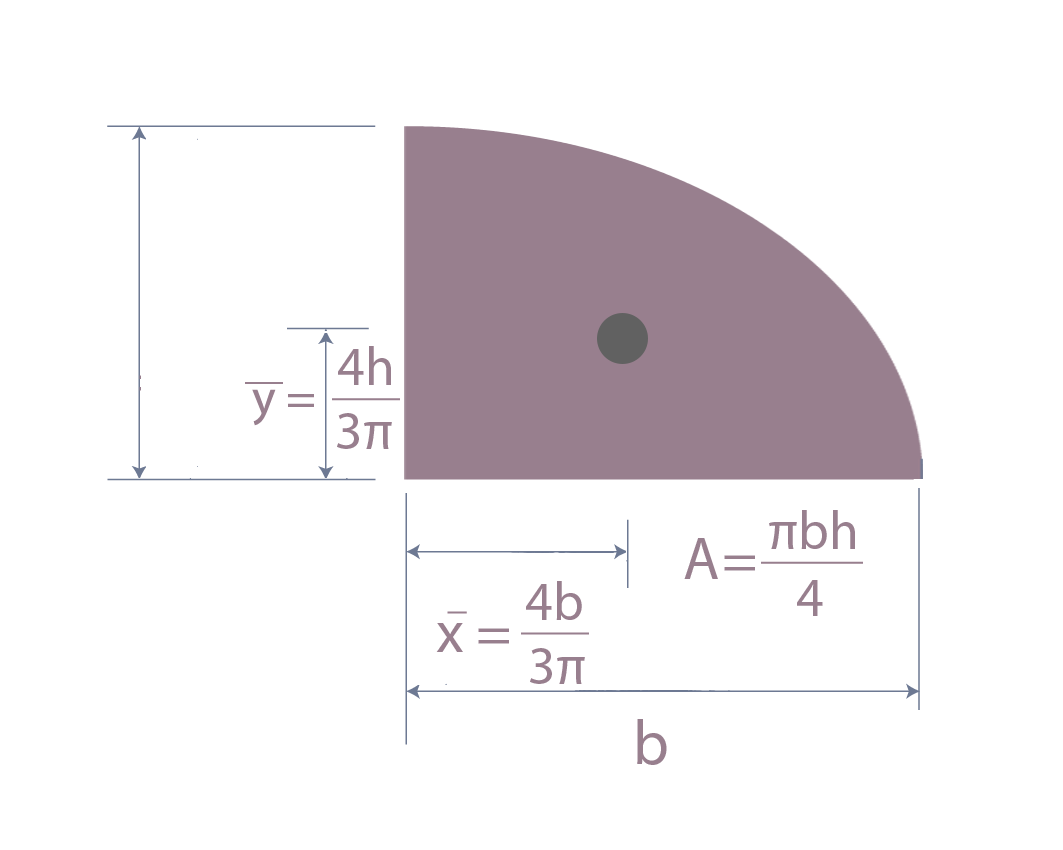
Coordenadas de centroide para elipse
Cuando h=b=r es círculo
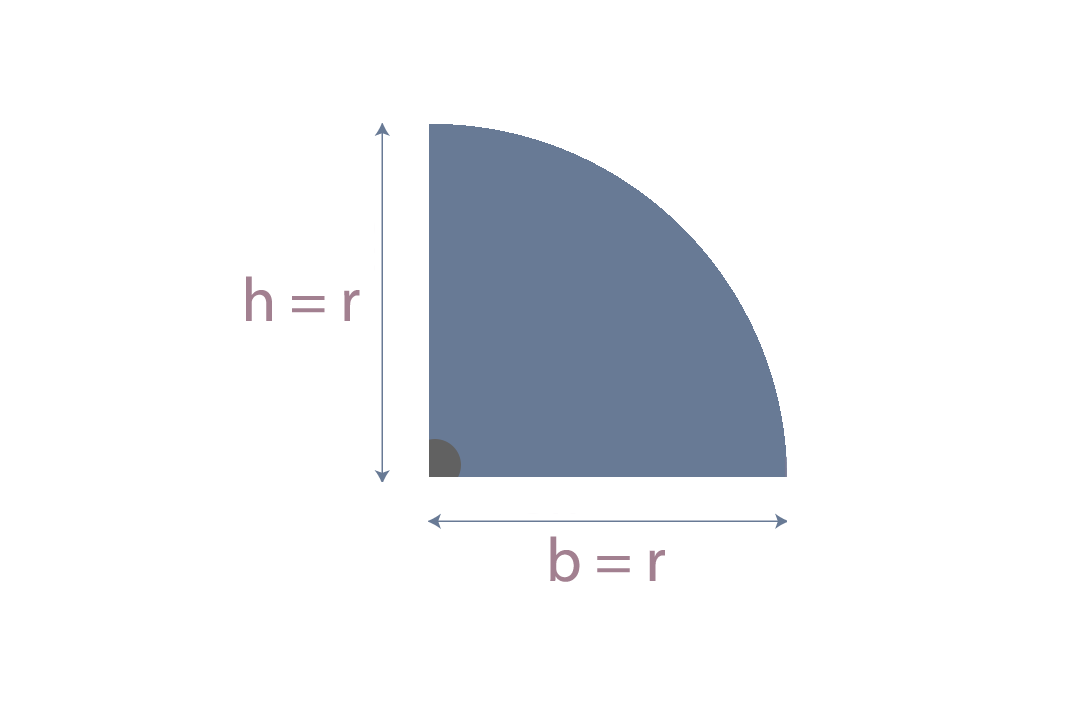
Coordenadas de centroide para círculo
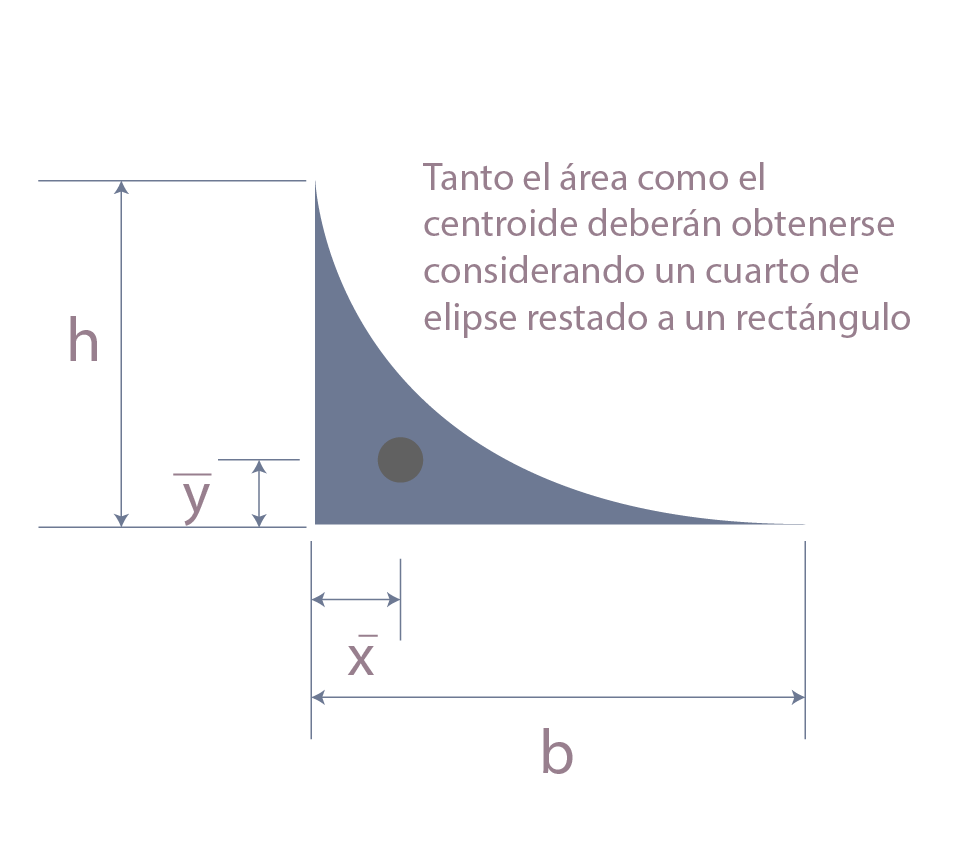
Coordenadas de centroide para ¼ de elipse
Como notaste, en las figuras anteriores las coordenadas de los centroides se tomaron a partir de la esquina inferior izquierda, esto nos indica la aplicación del primer cuadrante cartesiano.
Ahora, observa el siguiente gráfico, ¿cuál es el primer cuadrante?
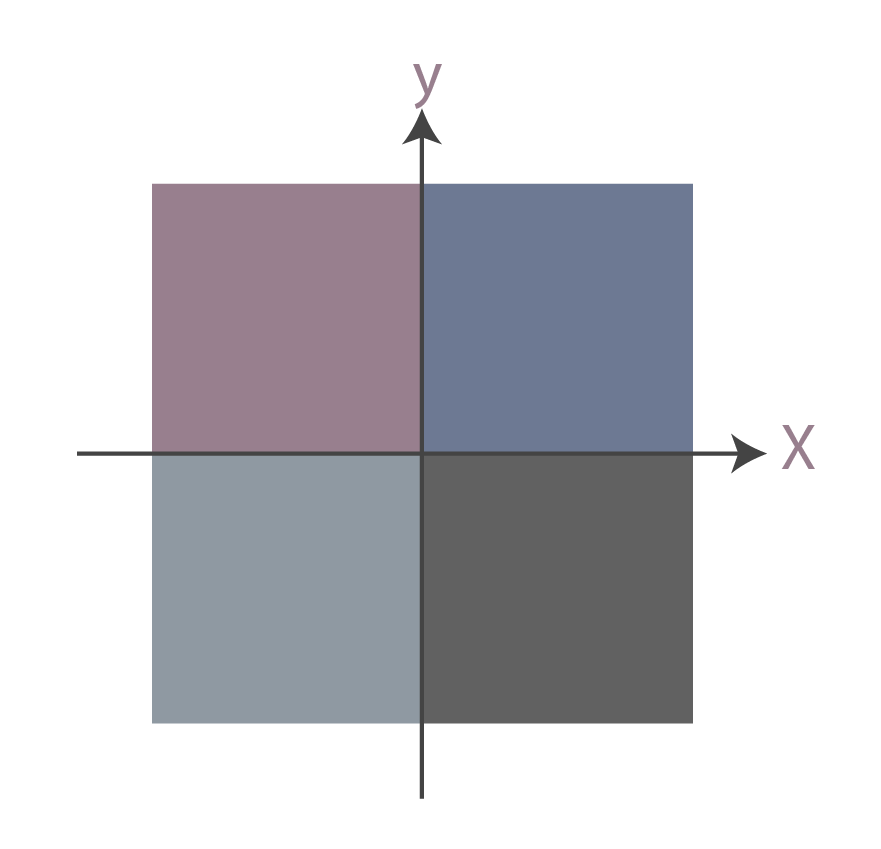
Con el objeto de poner en práctica el formulario expuesto con anterioridad, se realizará el siguiente ejemplo numérico para la obtención del centroide de un triángulo.
Pero ¿qué sucede si te encuentras con una figura en la que no se detectan formas regulares claras, como la siguiente?
Esquema de figura compleja
Este tipo de figura podría ser el resultado, por ejemplo, del diseño de una planta arquitectónica cualquiera.
En este caso, para obtener el centroide o centro de área de figuras complejas, como la anterior, se realiza lo siguiente:
El primer paso consiste en analizar el problema con el fin de proponer un esquema de trabajo adecuado, para lo cual, siempre debe tratar de resolverse en la menor cantidad de operaciones aritméticas; con esto se garantiza la posibilidad de reducir los márgenes de error.
El segundo paso corresponde a establecer los ejes cartesianos, de tal manera que la figura a resolver quede ubicada en el 1.er cuadrante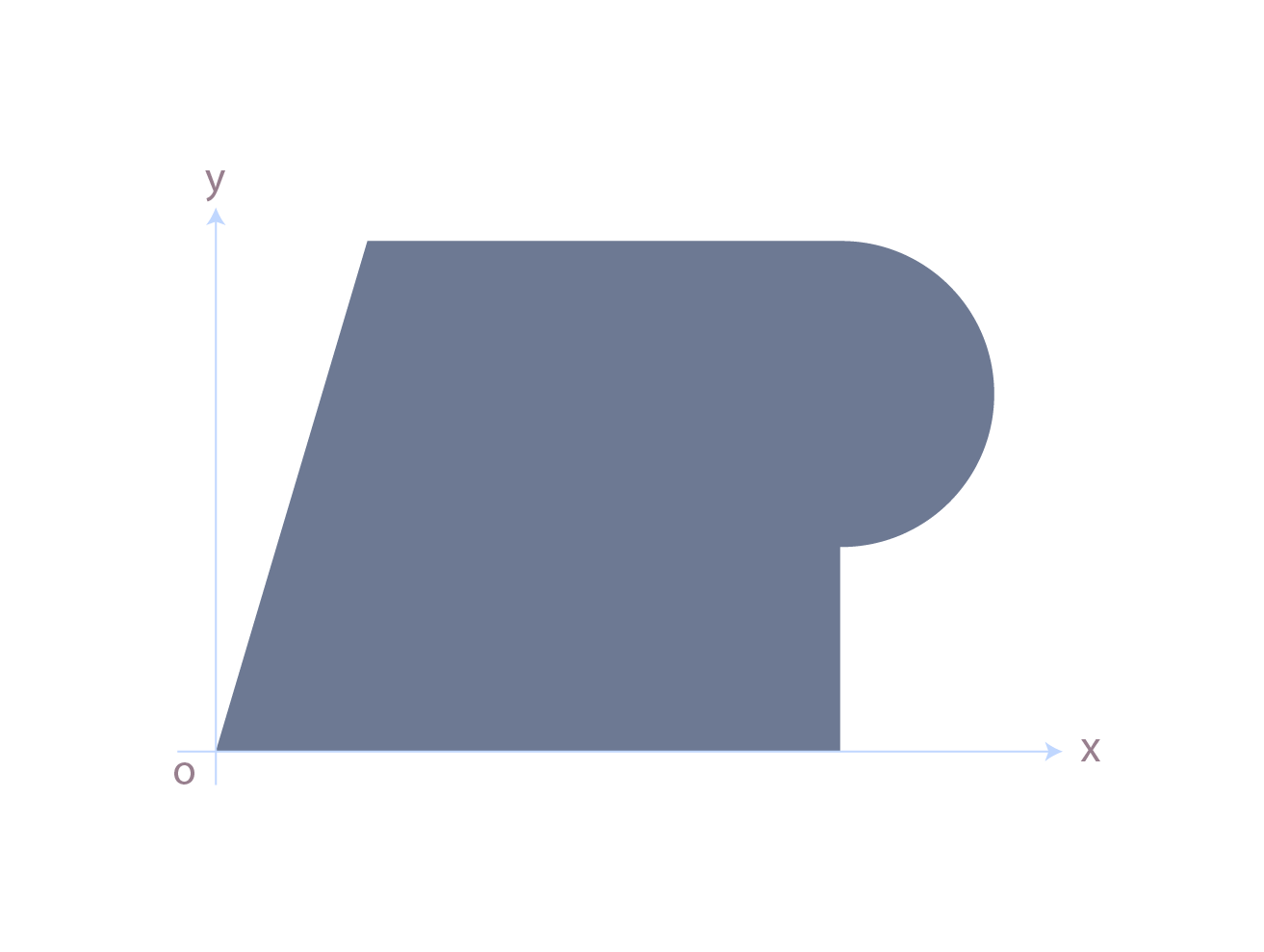
Figura compleja ubicada en el 1.er cuadrante del plano cartesiano .
El tercer paso consiste en subdividir la figura en formas geométricas regulares (por lo general: rectángulos, partes de elipse, triángulos y rectángulos.)
Es momento de poner en práctica el procedimiento para obtener centroides en figuras complejas.
En el cuarto paso es preciso clasificar las áreas parciales (asignar números o letras); reconocer el centroide de cada una de ellas y acotarlos de manera visible, de tal forma que se localicen, rápidamente, en el momento de aplicar las ecuaciones correspondientes. Las cotas a los ejes cartesianos deberán ser muy claras.
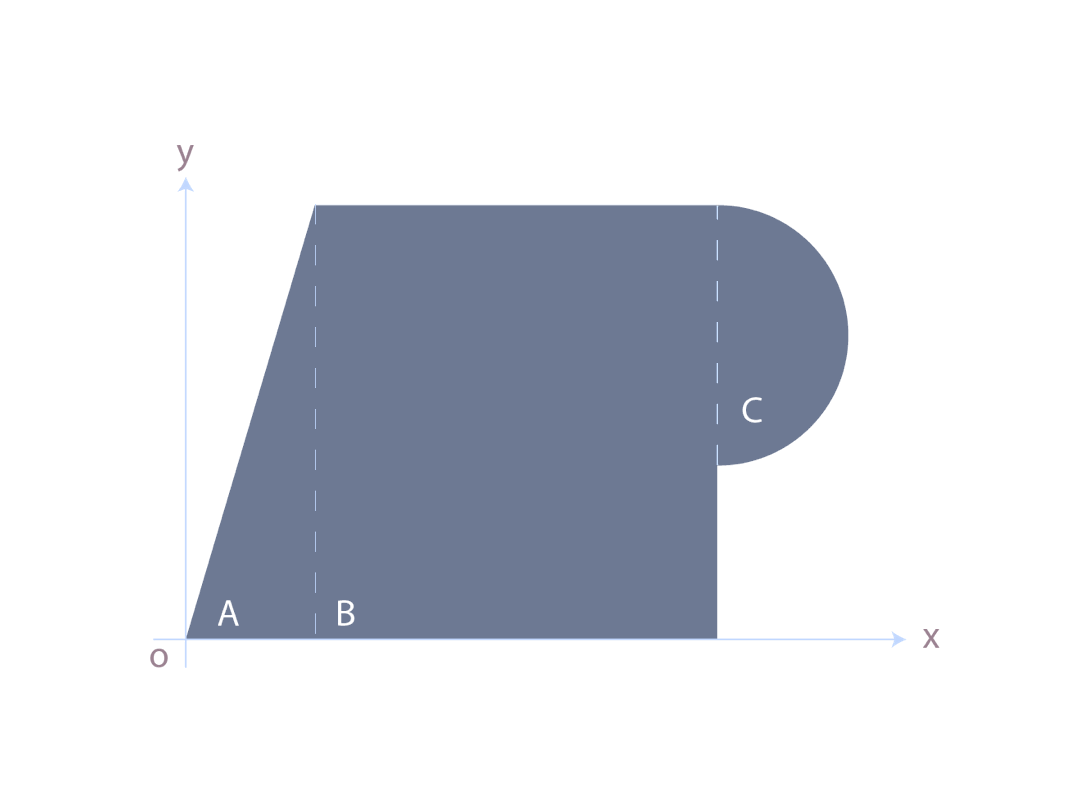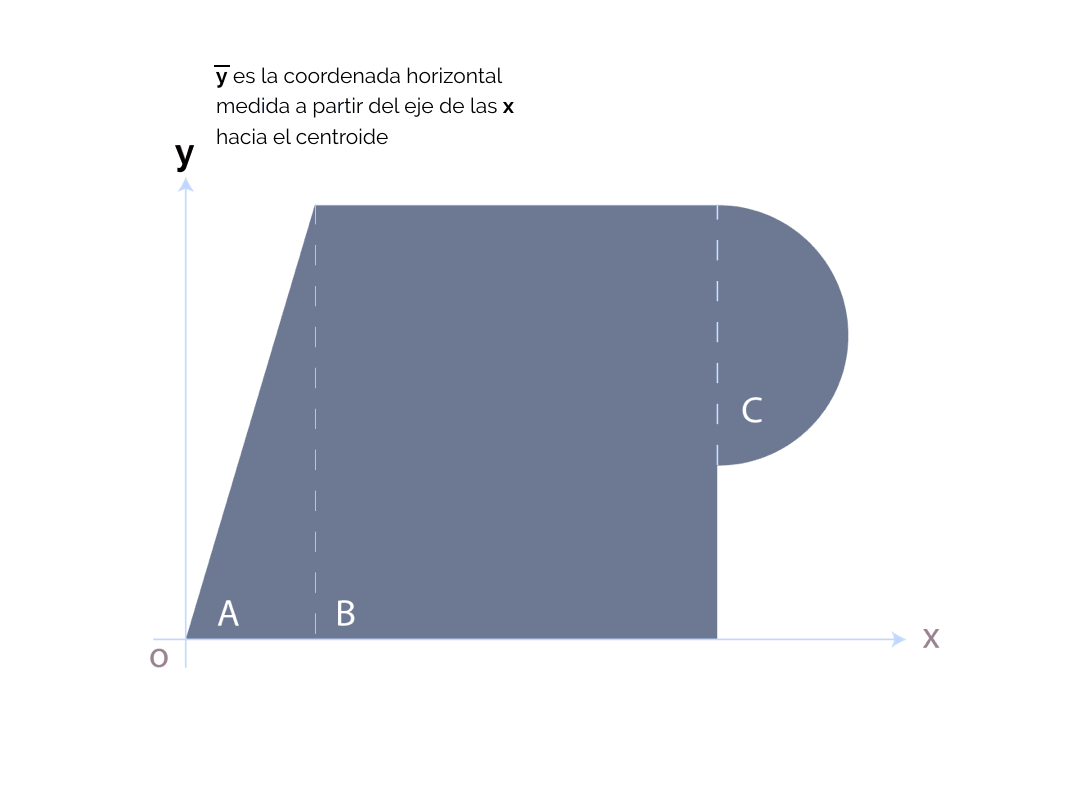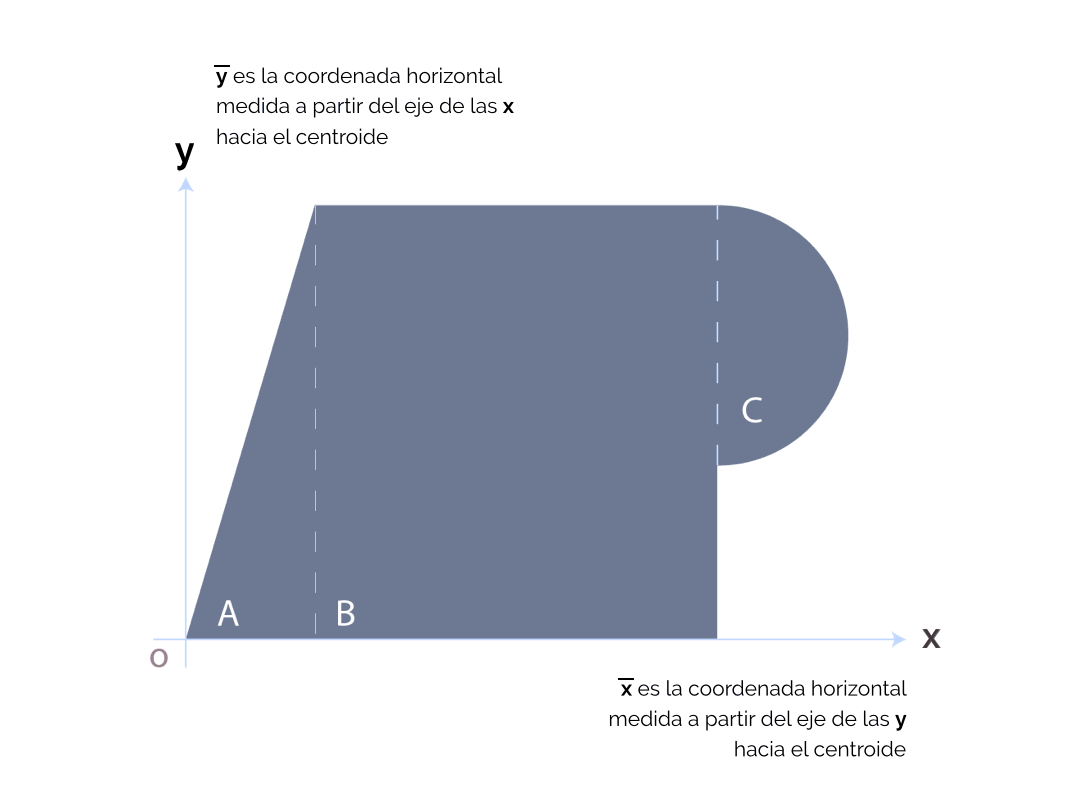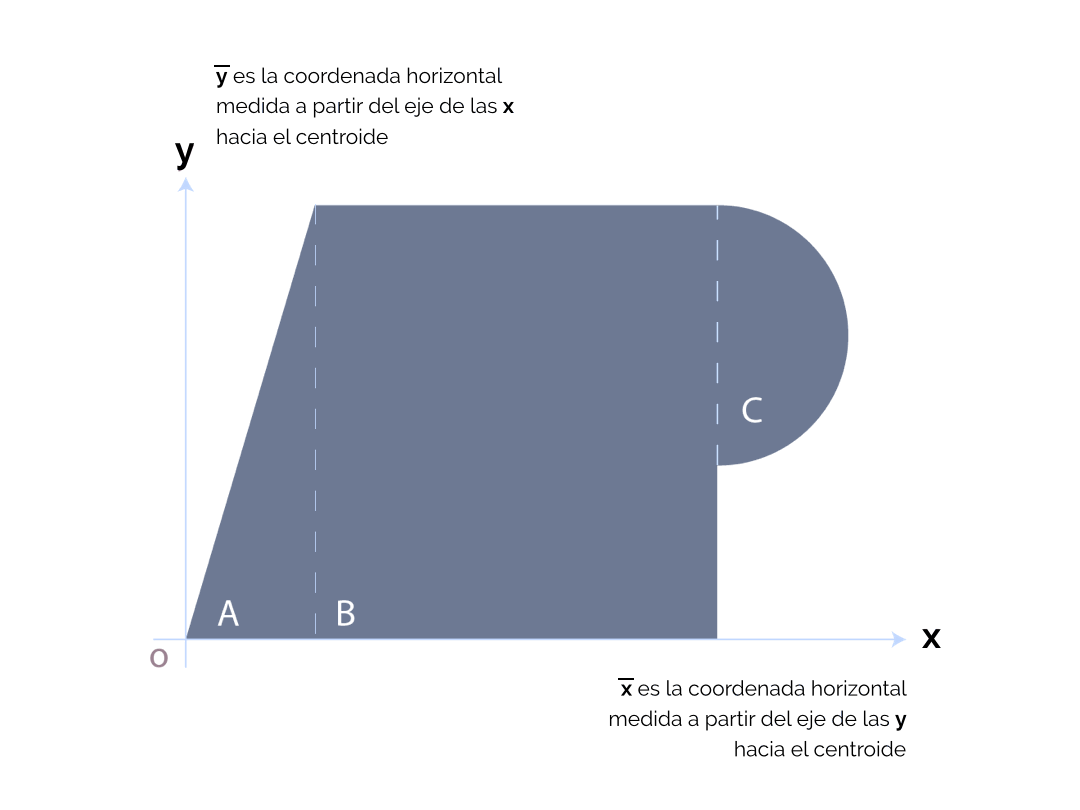
Las ecuaciones de la estática (∑F = 0; ∑M = 0) establecen, en principio, que, con la suma de áreas de las figuras, se realiza la ecuación en la que el área que equilibra, precisamente, será igual a dicha suma:
∑Áreas – Área equilibrante = 0,
donde Área equilibrante = ∑Áreas, tanto en el sentido de las x, como en el de las y.
En otras palabras, la equilibrante se opone a la resultante;
y con la suma de momentos, se tiene que:
∑Momentos – Momento equilibrante = 0
y como este momento equilibrante es igual al Área equilibrante (conocida), multiplicada por la distancia (incógnita) [Ad], se tiene que:
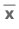= ∑My/∑Áreas
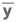= ∑Mx/∑Áreas
Así que vamos a concentrarnos en la obtención de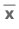, que es la coordenada horizontal, medida a partir del eje de las y.
Figura compleja donde se obtendrá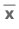
En el quinto paso se debe obtener el área de cada subdivisión y las ∑Áreas:
Figura compleja subdividida para obtener áreas
Área de la figura A (triángulo) = bh/2
AA = 2.2M(6.36M) /2 = 7.00M2
Área de la figura B (rectángulo) = bh
AB = 5.96M (6.36M) = 37.91M2
Área de la figura C (medio círculo) = Π r2/2
AC = ∏ (2.20M)2/2 = 7.60M2
∑Áreas = AA + AB + AC = 7.00M2 + 37.91M2 + 7.60M2 = 52.51M2
Para obtener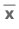es necesario calcular el momento estático de cada figura (Ad), para lo cual en el sexto paso es imprescindible ubicar sus centroides individuales y referirlos al eje de las y.
Figura compleja con centroides por subdivisión
Para obtener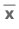
∑My/∑A con el momento de cada figura parcial:
MA = 7.00M2(1.47M) = 10.29M3
MB = 37.91M2 (5.18M) = 196.37M3
MC = 7.60M2 (9.09M) = 69.08M3
∑My = 275.74M3
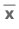= 275.74M3/52.51M2
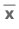= 5.25M
Los seis pasos que has revisado, hasta ahora, te han permitido desfragmentar la figura original, con el objeto de realizar las ecuaciones estáticas indicadas. Hasta este punto, hemos encontrado la coordenada
; así que hay un último paso que te permitirá saber el valor de
, con el cual ya estaremos en posibilidad de ubicar el centroide.
Ahora, ¿qué sucede si decides aplicar el conocimiento que has construido a lo largo de este repaso a un objeto de la cotidianeidad arquitectónica, como un perfil metálico en forma de ángulo?
Fuentes de información
González, I. (2017). Sistemas Estructurales Básicos. México: Instituto Politécnico Nacional (en prensa).
Carmona y Pardo, M. (1983). Estática en arquitectura. México: Trillas.
Cómo citar
González, I. (2018). Método analítico para obtener centroides de áreas. Unidades de Apoyo para el Aprendizaje. CUAED/Facultad de Arquitectura-UNAM. Consultado el (fecha) de (vínculo)
