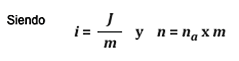¿Que son y cómo calcular las anualidades?

Unidad de Apoyo para el Aprendizaje

Iniciar

Introducción


Las anualidades resultan familiares en la vida diaria: rentas, sueldos, seguro social, pagos a plazos y de hipotecas, primas de seguros de vida, pensiones, aportaciones a fondos de amortización, alquileres, jubilaciones, etcétera. Si bien una anualidad es una sucesión de pagos, depósitos o retiros generalmente iguales que se realizan en periodos regulares de tiempo y con un interés, hay varios tipos de anualidad y diferencias entre cada tipo. Ante la importancia de los pagos periódicos y su cálculo de manera cotidiana, en esta unidad conocerás el funcionamiento de las anualidades, su método de cálculo y algunos ejemplos.



cálculo de anualidad


[Cálculo de anualidad] [fotografía]. Tomada de https://ujg1i3ze1133y9zav35eixy117m-wpengine.netdna-ssl.com/wp-content/uploads/2015/03/how-to-pay-yourself-as-a-small-business-owner-featured.jpg



Calcular las anualidades a partir de variables como el tiempo, interés o monto, y conocer su clasificación, funcionamiento e importancia en los créditos e inversiones que se realizan diariamente.

Anualidad


Los pagos realizados e ingresos percibidos por la empresa son de vital importancia; por ello, se deben medir constantemente.


¿Qué es la anualidad?

Anualidad




La palabra anualidad no implica que las rentas sean anuales, sino que se da a cualquier secuencia de pagos, iguales en todos los casos, a intervalos regulares, independientemente de si son anuales, semestrales, trimestrales, mensuales, quincenales o semanales.

Cuando en un país hay relativa estabilidad económica, es frecuente que se efectúen operaciones mercantiles a través de pagos periódicos; pueden hacerse con interés simple o compuesto, como en el caso de las anualidades.

En préstamos (por ejemplo, para adquisiciones de bienes), generalmente los pagos efectuados son iguales en intervalos y todo indica que la medida común es un año, a menos que se indique lo contrario. A veces son quincenales, mensuales, bimestrales, trimestrales, tanto para tasas como para pagos en el tiempo; cuando esto ocurre, se habla de convertibilidad de las tasas, ya que coinciden tiempo, tasa y pago de la deuda.

Significado de anualidad

Significado de anualidad



Anualidad

Es una sucesión de pagos, depósitos, abonos o retiros iguales que se realizan a intervalos iguales con interés compuesto.

Intervalo

También conocido como periodo de pago o periodo de renta; es el tiempo que transcurre entre un pago y otro.

Renta

Es el pago periódico que se hace o se recibe.

Plazo de una anualidad

Es el tiempo que transcurre entre el inicio del primer pago y el final o último.


Las anualidades son simples si los intervalos de pago son iguales en magnitud y coinciden con capitalización de los intereses.

Generales

Son de este tipo cuando los intervalos de pago y los periodos de capitalización de interés no son iguales.

Ciertas

Son de este tipo cuando sus fechas son fijas y se estipulan de antemano.

Contingentes

Son de este tipo cuando la fecha del primer pago, la fecha del último pago o las dos no se fijan de antemano; depende de algún hecho que se sabe ocurrirá, pero no se sabe cuándo.

Vencidas

Son de este tipo cuando se pagan al final del periodo.

Anticipadas

Son de este tipo cuando se pagan al inicio del periodo.

Inmediatas

Son los casos más comunes; la realización de los cobros o pagos tiene lugar en el periodo que sigue inmediatamente al trato.

Diferidas

Se pospone la realización de los cobros o pagos.


Para nombrar a la anualidad, también se utilizan los términos renta, pago periódico, abono y otros.

Algunos ejemplos de anualidades son los salarios quincenales o mensuales, fondos de amortización y depreciación, pagos a plazos, pensiones, pagos de primas de pólizas de seguros de vida o de automóviles, rentas producidas por los fondos de un fideicomiso, pagos para amortizar créditos hipotecarios, etcétera.

Clasificación de las anualidades


Los pagos de una anualidad se pueden hacer al inicio o al final del periodo, o también en sucesivos periodos intermedios. Puede ser que el periodo de capitalización coincida o no con el pago. Por estas razones y otras variantes, y con base en ciertos criterios, las anualidades se clasifican como sigue:



Tipos de anualidad

Criterio Tipo
Intereses Simples ---------- Generales
Tiempo Ciertas ----------- Contingentes
Pagos Ordinarias ------- Anticipadas
Iniciación Inmediatas ------ Diferidas

Tipos de anualidad

Descripción de los tipos de anualidades


Son aquéllas donde los periodos de pago coinciden con los de capitalización de intereses. En las generales, no coinciden; en las ciertas, se conocen con certeza las fechas del primer pago y del último; en las contingentes, puede no conocerse la fecha de iniciación, de terminación o ninguna.

Se llaman también vencidas; son aquéllas donde los pagos o depósitos se efectúan ordinariamente al final de cada periodo. Por ejemplo, un préstamo que se paga al final de cada periodo.

Los pagos o depósitos se realizan al principio de cada periodo. Por ejemplo, cuando se compra un bien y se da un enganche igual a cada pago.

Ocurren cuando el primer pago se realiza en el primer periodo de la operación financiera.

En ellas, existe un periodo llamado de gracia, donde se pospone el primer pago o depósito en un lapso convenido.

En ellas, se desconoce una o las dos fechas del plazo y no se pueden preestablecer. Por ejemplo, sobre la pensión de un derechohabiente no se sabe exactamente cuándo se jubilará ni cuándo dejará de cobrar (cuando muera, pero no se sabe cuándo morirá).

En ellas, los pagos son indefinidos, sin límite de tiempo. Por ejemplo, una persona o institución crea una beca mensual mediante la donación de un capital que se invierte y produce intereses, los cuales son precisamente la renta que se pagará.

Nomenclatura

C

Representa el capital inicial, llamado también principal. Suele representarse también por las letras “A” o “P” (valor presente).

M

Representa el capital final, llamado también monto o dinero incrementado. Es el valor futuro de “C”.

R

Es la renta, depósito o pago periódico.

J

Es la tasa nominal de interés calculada para un periodo de un año. Se expresa en tanto por uno o tanto por ciento.

I

Es la tasa de interés por periodo y representa el costo o rendimiento por periodo de capitalización de un capital, ya sea producto de un préstamo o cantidad que se invierte. Es el cociente de dividir la tasa nominal entre la frecuencia de conversión “m”.

m

Es la frecuencia de conversión o capitalización, y representa el número de veces que se capitaliza un capital en un año.

na

Es el número de años que permanece prestado o invertido un capital.

N

Es el número de periodos de que consta una operación financiera a interés compuesto.



Finalmente, para estudiar las anualidades a partir de su clasificación en cada caso, se deben resolver los siguientes problemas:


Pasos para considerar clasificación de anualidades

Pasos para clasificar un caso de anualidad



Es muy importante señalar que así como en el interés compuesto, donde las variables “n” (números de pagos) e “i” (tasa de interés) se expresan en la misma medida de tiempo, en las anualidades se agrega una variable, la renta (expresada como “R”), la cual debe estar también en la misma medida de tiempo.


Monto de una anualidad ordinaria


Una anualidad es ordinaria o vencida cuando los depósitos o pagos se hacen al final del periodo; para obtener el monto, se parte de su valor presente o capital.

El monto de las anualidades ordinarias o vencidas es la suma de los montos de todas y cada una de las rentas pagadas hasta el momento de realizar la última.



Ejercicio 1, anualidad

Ejercicio 1 de monto de anualidad



Tabla de conceptos

Ejercicio 1 de tabla de concepto



Ahora bien, si el monto total es igual a la suma de los montos de cada anualidad, llegaremos al mismo resultado:



Tabla de montos

Tabla de montos



Fórmulas para calcular el monto futuro de una anualidad simple, cierta y ordinario

Se conoce la renta, tasa nominal, frecuencia de conversión y plazo de tiempo:



Fórmula 1 cálculo de anualidad


Fórmula 1 para cálculo de monto futuro de anualidad simple

Fórmula 2 cálculo de anualidad


Fórmula 2 para cálculo de monto futuro de anualidad simple



Si se aplica la fórmula anterior a los datos del ejercicio 1, se tiene lo siguiente:

Ejercicio 2

Ejercicio 2



Ejercicio 3

Ejercicio 3



Valor actual de una anualidad ordinaria


Cuando la época del cálculo coincide con la iniciación de la serie de pagos o rentas, el valor equivalente de la serie es actual. El lapso que transcurre entre la fecha de la entrega del valor actual y el vencimiento de la primera anualidad será igual a cada periodo que separa a las demás rentas.

El valor presente o actual de las anualidades ordinarias se puede presentar en alguna de estas dos modalidades:


Modalidades de anualidades ordinarias

Modalidades del valor presente o actual



Se tienen seis pagarés con vencimientos escalonados en forma trimestral, cada uno de 25 000 pesos, y se quieren liquidar el día de hoy; la tasa es de 6 % trimestral.


Ejercicio 4

Ejercicio 4



Se determina el valor actual o presente de cada documento:



Valor actual o presente

Determinar valor actual o presente



Ahora bien, ¿qué cantidad habrá que invertir a 6 % cuatrimestral para tener derecho a recibir seis rentas de 25 000 pesos cada una? De acuerdo con la resolución anterior, se sabe que el valor actual es de 122 933.10. Hay que comprobar si con el importe de seis pagos de 25 000 pesos cada uno, el deudor salda su cuenta.



Ejercicio 4 conceptos

Conceptos



Por redondeo de cifras


Con base en lo anterior, se debe encontrar el valor actual de cada pago para determinar el valor presente total de la serie de rentas. Es posible decir que el valor actual es igual a la suma de los valores actuales de cada renta.

Fórmulas para calcular el valor presente de una anualidad simple, cierta, ordinaria


Fórmula valor presente

Fórmula para cálculo de valor presente



Ejercicio 5

Ejercicio 5



Ejercicio 6

Ejercicio 6



Monto de interés compuesto

Ejercicio 6 de monto de interés compuesto



Fórmulas para calcular la renta de una anualidad simple, cierta y ordinaria


Si se conoce el capital inicial, tasa de interés nominal o por periodo de capitalización, frecuencia de conversión y plazo o número de periodos de capitalización, se utiliza esta fórmula:


Fórmula renta de anualidad

Fórmula para cálculo de anualidad simple, cierta y ordinaria



Si se conoce el monto futuro, tasa de interés nominal o por periodo de capitalización, frecuencia de conversión y plazo de tiempo o número de periodos de capitalización, se utiliza esta fórmula:


Fórmula monto futuro

Fórmula en caso de saber monto futuro



Ejercicio 7

Ejercicio 7



Ejercicio 8

Ejercicio 8



Cálculo mes 4

Cálculo del cuarto mes



Ejercicio 9

Ejercicio 9



Fórmulas para calcular el tiempo o plazo en una anualidad simple, cierta, ordinaria


Si se conoce el capital inicial, renta, tasa nominal o tasa efectiva por periodo y frecuencia de conversión, se utiliza esta fórmula:


Fórmula tiempo o plazo

Fórmula para cálculo de tiempo o plazo



Si se conoce el monto futuro, renta, tasa nominal o tasa efectiva por periodo y frecuencia de conversión, se utiliza esta fórmula:


Fórmula si se conoce monto futuro

Fórmula para cálculo de tiempo o plazo si se conoce monto futuro



Ejercicio 10

Ejercicio 10



Ejercicio 11

Ejercicio 11



Ejercicio 11, monto de último pago

Ejercicio 11, monto de último pago



Ejercicio 11, cinco pagos iguales y uno mayor

Ejercicio 11, cuando existen cinco pagos iguales y uno mayor



Fórmulas para calcular la tasa de interés de una anualidad simple, cierta y ordinaria


Debido a que la tasa de interés se encuentra en el numerador y el denominador de las fórmulas de monto y valor actual de una anualidad simple, cierta u ordinaria, no se puede despejar; por ello, se utiliza para su cálculo el procedimiento llamado de prueba y error a base de iteraciones sucesivas.

También se puede utilizar una calculadora programable, financiera o una computadora con software financiero.

Si se conoce el capital inicial, renta, frecuencia de conversión y plazo de tiempo o número de periodos de capitalización, se utiliza esta fórmula:


Fórmula tasa de interés de anualidad

Fórmula para cálculo de tasa de interés anual



Si se conoce el monto futuro, renta, frecuencia de conversión y plazo de tiempo o número de periodos de capitalización, se utiliza esta fórmula:


Fórmula tasa de interés de anualidad con monto futuro

Fórmula para tasa de interés de anualidad con monto futuro



Ejemplo 12

Ejemplo 12



Ejemplo 13

Ejemplo 13



Ejemplo 13, calculo tasa nominal y efectiva

Ejemplo 13, cálculo de tasa nominal y efectiva anual



Ejercicio 14, cinco pagos iguales y uno mayor

Ejercicio 14



Ejemplo 13, calculo tasa nominal y efectiva

Ejemplo 13, cálculo de tasa nominal y efectiva anual



Ejemplo 14, calculo tasa nominal y efectiva

Ejemplo 14, cálculo de tasa nominal y efectiva anual



En conclusión, el conocimiento del concepto de anualidades y sus principales características permite conocer la aplicación cotidiana de las anualidades en la toma de decisiones de inversión y crédito.


Actividad. Cálculo de anualidades en inversiones y crédito

La claridad y precisión en los ingresos o deudas en términos de valor presente y valor futuro te permitirá planear tus finanzas personales en términos de cuánto dinero recibirás en algún momento del tiempo, o cuánto deberás pagar a una fecha determinada; ante dicha situación, es muy importante un conocimiento pleno del funcionamiento de las anualidades.

Autoevaluación. Funcionamiento de la anualidad en las transacciones financieras cotidianas

Ahora que ya conoces lo que son las anualidades, su funcionamiento, clasificación y cálculo de las mismas a partir de algunas de sus variables (tiempo, interés o monto), realiza la siguiente autoevaluación.

Fuentes de información

Básicas

Bibliografía

Díaz, M. A. (2013). Matemáticas financieras (5.a ed.). México: McGraw-Hill.

Dumrauf, G. L. (2013). Matemáticas financieras. México: Alfaomega.

Rodríguez, F. J. (2015). Matemáticas financieras con aplicaciones en Excel. México: Patria.

Vidaurri, A. H. (2012). Matemáticas financieras (5.a ed.). México: Cengage Learning.

Villalobos, J. (2012). Matemáticas financieras (4.a ed.). México: Pearson.

Documentos electrónicos

Camargo, A., Pompa, M., Mata, J. y Viveros, P. (2016). Matemáticas Financieras [Versión electrónica]. México: UNAM. Consultado el 23 de enero de 2019 de http://fcasua.contad.unam.mx/apuntes/interiores/docs/20172/contaduria/1/apunte/LC_1154_14116_A_MatematicasFinancieras.pdf

Complementarias

Bibliografía

Haeussler, E. F. (2015). Matemáticas para administración y economía (13.a ed.). México: Pearson.

Mora, Z. A. (2012). Matemáticas financieras (3.a ed.). México: Alfaomega.

Rodríguez, F. J. (2014). Matemáticas financieras 2. México: Patria.

Sydsaeter, K. (2012). Matemáticas para el análisis económico (2.a ed.). Madrid: Pearson.


Cómo citar

Morales, A. (2019). ¿Qué son y cómo calcular las anualidades? Unidades de Apoyo para el Aprendizaje. CUAED/Facultad de Contaduría y Administración-UNAM. Consultado el (fecha) de (vínculo).